Omyl pana Bolča

Jan Erben

Pan Bolčo se ve svém článku dopouští elementárních chyb, založených na standardním opomenutí většiny Einsteinových "vyvracečů” : Používá stejné označení pro různé veličiny a naopak tím, že zaměňuje rozdíl souřadnic měřených v různých vlastních časech se vzdáleností. Pak pochopitelně může dojít k paradoxním závěrům.

Konkrétně zde použil označení x₀ pro počáteční posunutí, které je pevné v S (obr.2), a které tedy (správně) v S’ má potom velikost x₀/g (obr.3). Dále ovšem použil na obr.5 označení x₀’ pro počáteční posunutí, které je pevné v S’ – ve skutečnosti vzhledem k symetrii musí být počáteční posunutí (interpretované jako pevné v příslušné IS) stejné v obou soustavách S a S’ , tedy na obr.5 mělo být -x₀ místo -x₀’, a tedy na obr.6 má být -x₀/g místo –x₀’/g. Je sice vhodné v L.T. s počátečním posunutím x₀ zůstat v S' u označení x₀', aby bylo zřejmé, kde posunutí odečítáme, nicméně je dobré si uvědomit, že v tomto případě jde o souřadnici a nikoliv o pevnou vzdálenost a nelze pro ni použít vzorec pro kontrakci ! Uvědomíme-li si, že x₀’ = x₀/g je pevná vzdálenost x₀ měřená v soustavě, která se vůči x₀ pohybuje (Lorentz-Fitzgeraldova kontrakce), je ihned zřejmé, jak touto záměnou dospějeme k paradoxnímu závěru x₀ = x₀’/g, tedy ke sporu pro g různé od 1. Dále souřadnice x na obr. 2 není obecně rovna souřadnici x na obr.6, podobně pro obr.3 a 5.

Jak to má správně být ?

Např. na obr.2 naměří pozorovatel v S vzdálenost x₁ = x₀ + v.t + x’/g (je-li A pevný bod v S’)
za vlastní čas t od okamžiku, kdy počátek S’ projde bodem o souřadnici x₀ na ose x v S.

Zatímco na obr.6 naměří pozorovatel rovněž v S jinou vzdálenost x₂ = x₀/g + v.t + x’/g (opět je-li A pevný v S’)
za stejný vlastní čas t, ovšem tentokrát od okamžiku, kdy počátek S projde bodem o souřadnici –x₀/g na ose x’ v S’ ! Protože x₀/g < x₀, je také pochopitelně x₂ < x₁ a to právě o rozdíl x₀ – x₀/g , aniž by to nějak překvapovalo – časy t jsou sice stejné, avšak okamžiky počátku odměřování času t různé ! Rozdíl x₁-x₂ představuje L.F. kontrakci délky měrné tyče x₀, je-li pevná v S’, z pohledu S. Tyto různé délky označuje ovšem Bolčo stejným symbolem x.






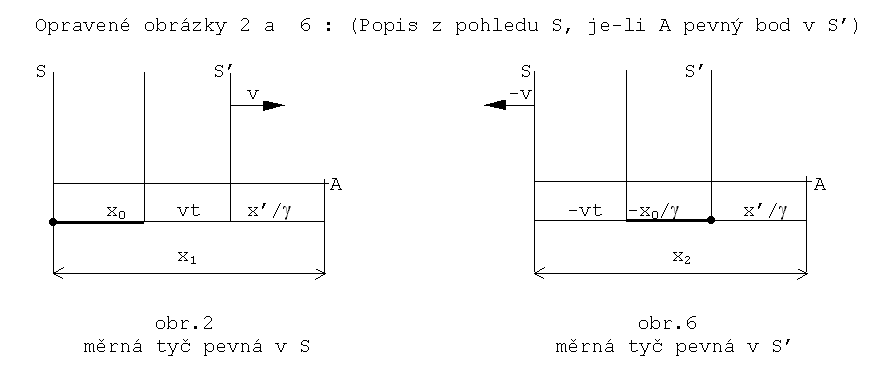
Pan Bolčo tedy jednak použil na obr.5 a 6 jiné označení x₀’ tam, kde mělo být x₀ jako na obr.2 a 3, jednak použil stejné označení x pro různé délky x₁ a x₂.

Podobně v S’ :
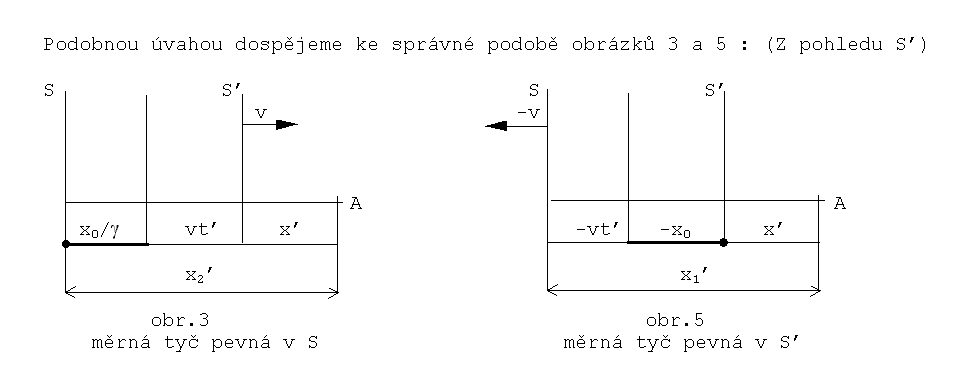
Rozdíl vzdáleností x₁’– x₂’ naměřený pozorovatelem v S’ po vlastním době t’ je opět roven rozdílu délek x₀ – x₀/g a opět odpovídá kontrakci délky měrné tyče x₀, tentokrát z pohledu S’ , je-li pevná v S.

Na všech obrázcích symbolizuje černé kolečko spojení pevné “měrné tyče” o délce rovné počátečnímu posunutí x₀ s příslušnou IS (S na obr.2 a 3, S’ na obr.6 a 5), jak to zavedl pan Bolčo.

Uveďme ještě pro přesnost, že i shora uvedené úvahy platí pouze ve speciálním případě, kdy délka úseku x’ představuje prostorupodobný interval konstantní délky, kdy lze pro něj užít vzorec pro kontrakci délky x’/g, tedy za předpokladu, že bod A je pevným bodem v S’. Pak ovšem tento bod není pevným bodem v S, což je zase podmínkou toho, aby vzdálenost označená panem Bolčem na obr.2 a 6 jako x byla prostorupodobným intervalem konstantní délky, chceme-li pro její vyjádření v S’ užít vzorec pro kontrakci délky x/g, jak to Bolčo činí na obr. 3 a 5. Je tedy zřejmé, že x a x’ nemohou být současně konstantními intervaly, tedy buď platí x’/g na obr.2 a 6, nebo platí x/g na obr.3 a 5, nikoliv však obojí současně. V obecném případě ovšem nejsou konstantními intervaly ani x ani x’ , a tedy pro ně nelze užít vzorec pro kontrakci délky – je nutno užít vzorec pro transformaci souřadnic :

Pro jednoduchost se omezíme na transformaci polohových souřadnic.

Při odvození tohoto vzorce můžeme postupovat např. následujícím způsobem :

a) Začneme se standardní situací bez počátečního posunutí (obr.A)




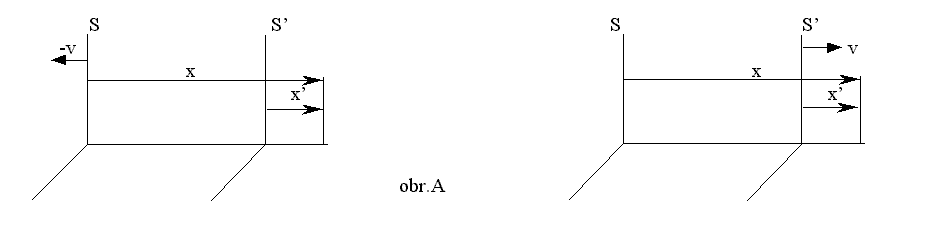
Zde platí známé speciální Lorentzovy transformace

(A1) x = g.(x’ + vt') (A2) x’= g.(x – vt)

o jejichž symetrii snad nepochybuje ani pan Bolčo !

b) odvoďme transformační vzorec pro přechod od x k x’ se zahrnutím počátečního posunutí x₀ v čase t = 0 v S.
Za tím účelem zavedeme pomocnou soustavu S’’ , pohybující se spolu s S’ rychlostí v vzhledem k S, jejíž počátek v čase t = 0 splývá s počátkem S (obr.B).




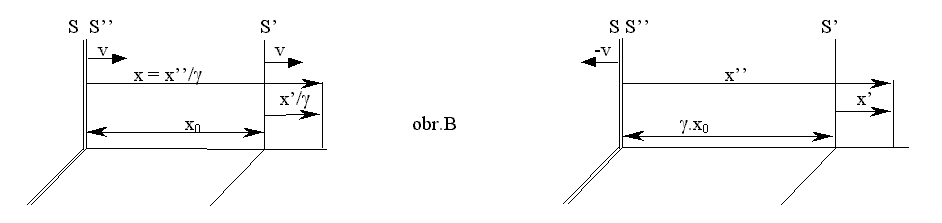
Zde je pohled v t = 0 v S, v něm platí                                 Zde je pohled v t = 0 v S’ , v něm platí

x’’ = g.(x – vt) dle (A2)                                                       x’’ = x’ + g.x₀
(v S je vzdálenost počátku S’ a S’’ x₀)                               protože v S’ je vzdálenost počátků S’a S’’ g.x₀

(1) celkem dostáváme x’ = g(x – x₀ – vt) , kde x₀ je počáteční posunutí v S  v  t = 0.

c) odvoďme transformační vzorec pro přechod od x’ k x se zahrnutím počátečního posunutí x’₀ v čase t’ = 0 v S’.
Za tím účelem zavedeme pomocnou soustavu S₁ , pohybující se spolu s S vzhledem k S’ rychlostí -v , jejíž počátek v čase t’ = 0 splývá s počátkem S’ (obr.C). Upozorněme především, že obecně neplatí ani x’₀ = x₀/g, ani x’₀ = x₀. Počáteční posunutí závisí na volbě okamžiku t’ = 0. Při vhodné volbě (takové, abychom dostali jednoduché symetrické transformační vztahy) bude ovšem x₀ = x’₀, přesto ponecháváme označení x’₀, abychom znázornili, v jaké soustavě počáteční posunutí měříme.




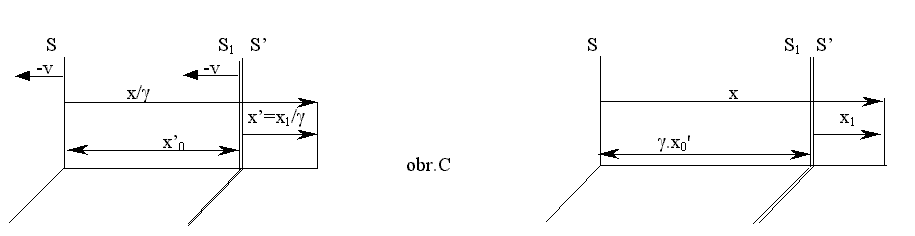
Zde je pohled v t’ = 0 v S’ , počátky                                         Zde je pohled v t’ = 0 v S, počátky S,S₁
S,S₁ jsou vzdáleny z pohledu S’ o x’₀                                   jsou tedy v klidu vzdáleny více : g.x’₀
zde platí pro přechod od S’ k S₁                                                 takže platí

x₁ = g.(x’ + vt') dle (A1)                                                        x₁ = x - g. x’₀

(2) celkem dostáváme x = g.(x’ + x’₀ + vt’) kde x’₀ je počáteční posunutí v S’  v  t’ = 0.

jak se ostatně dalo čekat.

Musíme si nyní uvědomit, že stanovíme-li např. pomocí (1) pro dvě souřadnice x₁ a x₂ polohy x’₁ a x’₂, pak tyto polohy v S’ představují souřadnice v různých vlastních časech t’₁ a t’₂ v S’. Zatímco tedy v S byly tyto souřadnice stanoveny ve stejném čase t a lze je tedy interpretovat jako geometrickou vzdálenost bodů o těchto souřadnicích v S, v S’ byly tyto souřadnice stanoveny v různých časech a nelze je tedy jako geometrickou vzdálenost interpretovat. Pan Bolčo ovšem s těmito pojmy (souřadnice, délka) operuje značně volně, ba přímo s nimi žongluje, a pak se nelze divit, k jak paradoxním závěrům dochází ! (Např. na našich obrázcích označují jednoduché šipky souřadnice, dvojité šipky pak vzdálenosti, přičemž S’ a S’’ na obr.B nebo S a S₁ na obr.C jsou vůči sobě v klidu, proto mají stejný vlastní čas.)

Ilustrujme si tuto myšlenku na jednoduchém problému odvození vzorce pro kontrakci délky, který nicméně velmi dobře ukáže podstatu chyby, již se dopouští pan Bolčo :

Mějme za úkol stanovit transformační vzorec pro délku tuhé tyče. Nechť tyč je pevně umístěna v soustavě S a má zde klidovou délku L. Stanovme její délku z pohledu soustavy S´, která se vůči S pohybuje rychlostí v. Můžeme postupovat dvěma způsoby :

d) Chceme-li stanovit délku tyče v soustavě, v níž se tyč pohybuje, musíme zajistit, abychom souřadnice konců tyče odečítali ve stejném čase t’ (obr.D). Jinak se během časového intervalu mezi odečty tyč posune a druhá souřadnice bude odečtena chybně. (To koneckonců platí i v klasické mechanice, takže by to snad nepřekvapilo ani pana Bolča.) Proto odečteme v S’ souřadnice x’₁ a x’₂ ve stejném čase t’. Pak z Lorentzovy transformace plyne pro souřadnice x₁ a x₂ v S :



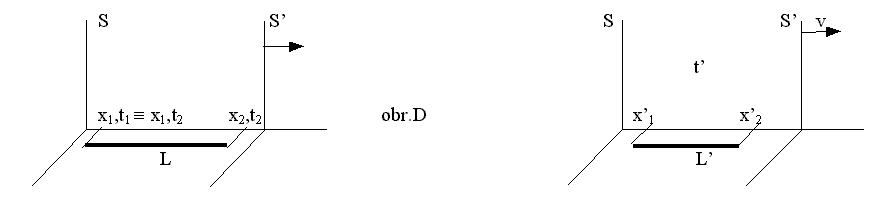
x₁ = g(x’₁ + vt’)                                                x₂ = g(x’₂ + vt’) a protože

(3) x₂ – x₁ = L                     a                              x’₂ – x’₁ = L’

(V S sice odečítáme souřadnice x₁ a x₂ v různých časech, to však není na závadu, protože tyč je v S pevně umístěna.)

dostáváme konečně :

(4) L = g.L’ , tedy pozorovatel v soustavě, v níž se tyč nepohybuje naměří délku tyče delší g-krát.

e) Můžeme ovšem postupovat i poněkud komplikovanějším přímým postupem od S k S’. Jsou-li L.T. transformace v pořádku, neměli bychom dojít ke sporu : Změřme tedy v S v určitém časovém okamžiku souřadnice konců tyče x₁ a x₂. Tomu odpovídají souřadnice konců tyče v S’ :

x’₁ = g(x₁ – vt) x’₂ = g(x₂ – vt)

(Nyní bychom mohli použít (3), zjistit, že pak L’ = x₂’ – x₁’ = g.L (obr.E) , což je ve zjevném rozporu s (4) a přesně to odpovídá situaci, v níž se ocitl pan Bolčo s délkami x₀ a x’₀ ! Vidíme, že ke stejnému paradoxu lze dospět s podstatně menším vynaložením energie a elementárních matematických cvičení, než potřeboval pan Bolčo.)

Kde je chyba ? Musíme si uvědomit, že souřadnice x’₁ a x’₂ byly tentokrát odečteny v různých časech

t’₁ = g(t – vx₁/c²) t’₂ = g(t – vx₂/c²) (t’₁ > t’₂ pro x₂ > x₁)

Za dobu Dt’ = t’₁ – t’₂ = g.v/c² .(x₂ – x₁) se tyč vzhledem k S’ posune o v.Dt’ = g.v²/c².L . Správnou délku tyče v S’ tedy dostaneme po odečtení tohoto posuvu (obr.E):




(5) L’ = x’₂ – x’₁ - g.v²/c².L = g.L - g.v²/c².L = g.(1 – v²/c²).L = g . g ^-2 .L = L/g

což přesně koresponduje se (4) !


Celý problém s dosti častým “vyvracením” STR laiky vyplývá podle mého názoru z toho, že potřebná matematika je na úrovni ZŠ, což mnohým laikům dává pocit, že STR rozumí. Nicméně skutečná obtížnost pochopení STR netkví v použité matematice, nýbrž ve zdánlivě paradoxních důsledcích, k nimž použití L.T. vede (kinematické paradoxy jako kontrakce délek, dilatace času, narušení současnosti nesoumístných událostí, skládání rychlostí, či dynamické paradoxy typu transformace hmotnosti). Přesné vysvětlení fysikální podstaty těchto jevů a schopnost ukázat, proč ve skutečnosti nevedou ke sporům a paradoxům leží v pozadí správného pochopení této dnes již mnohokrát experimentálně ověřené teorie.