 ČASOVÁ
NESYMETRIE VE FYZICE A NEVRATNOST DĚJŮ
ČASOVÁ
NESYMETRIE VE FYZICE A NEVRATNOST DĚJŮ ČASOVÁ
NESYMETRIE VE FYZICE A NEVRATNOST DĚJŮ
ČASOVÁ
NESYMETRIE VE FYZICE A NEVRATNOST DĚJŮ
Hodlám zde diskutovat problém, který mne zaujal při četbě práce (Elliott H. Lieb, Jakob Yngvason)[1]. Článek je opravdu velmi zajímavý (lze jej získat na webu na adrese archivu Los Alamos N.L. : http://xxx.lanl.gov/abs/condmat/9708200 - existuje i pozdější zkrácená a “popularisovaná” verse [2], WWW odkaz je u nás šířen i na serveru AmberZine).
Ovšem interpretací entropie z pohledu termodynamiky se zabývat nechci. Jedná se mi o statistickou interpretaci entropie a vůbec o otázku vratnosti a nevratnosti ve fysice. Výše zmíněná práce s tím souvisí spíš okrajově – autoři [1] zde vyjadřují pochybnost (pokud jsem neučinil chybu v překladu), že by zákon růstu entropie byl někdy opravdu odvozen prostředky statistické fysiky, tedy užitím aparátu mechaniky (ať již klasické či kvantové) a počtu pravděpodobnosti.
Ač jsem problém nikdy příliš podrobně nestudoval, žil jsem v domnění, že vysvětlení této souvislosti bylo přesvědčivě podáno již v pracích Maxwella a Boltzmanna, ba dokonce jsem se patrně naivně domníval (a stále domnívám), že podstata jevu, kdy procesy provázející vývoj makroskopických soustav částic, jejichž chování se řídí časově symetrickými rovnicemi, se nám jeví časově nesymetrické, je elementární a očividná. Když se mi pak do ruky dostala kniha (P. Coveney a R. Highfield) [3], byl jsem zmaten ještě více, neboť autoři přesvědčují čtenáře, že tento jev není doposud uspokojivě vysvětlen, ba dokonce, že bude nutno vyvinout k tomuto účelu nový matematický aparát. Mohl bych samozřejmě toto tvrzení hodit za hlavu s poukazem, že se vyskytuje v knize, která obsahuje takřka tolik vágních “filosofujících” formulací jako skutečných argumentů. Uznávám, že do jisté míry je to “vinou” nikoliv autorů, nýbrž populárního charakteru knihy, jemuž bylo nutno sloh přizpůsobit. Avšak rovněž dosti popularisující kniha [4] je dokladem, že to autoři [3] možná přehnali. Ke knize [3] se ještě vrátím v poznámce 1) v závěru. Nicméně názor profesora Lieba v [1] se asi jen tak za hlavu hodit nedá. Navíc se zdá, že se v poslední době opakuje historie sporu mezi “Boltzmannovci” a “Zermelovci” a objevují se další poněkud zmatené námitky k dříve prokázané souvislosti mikroskopické vratnosti a makroskopické “nevratnosti” .
Rád bych Vás teď seznámil s mým značně zjednodušeným pohledem na podstatu vratnosti a nevratnosti ve statistické fysice, o němž se nicméně domnívám, že není natolik zjednodušený, aby neplatil. Úvodní část argumentace v a) patří práci (prof. Lebowitze – odkaz rovněž na serveru LANL –http://xxx.lanl.gov/abs/condmat/9605183) [5], avšak v dalším se pokusím formulovat silnější variantu jeho závěrů, která, jak se mi zdá, lépe vystihuje původní smysl Boltzmannovy idey. Hlavní zjednodušení spočívá v tom, že se ignorují kvantové jevy a relativita. Domnívám se totiž, že lze ukázat (jak tvrdí i J.L.Lebowitz), že hlavním zdrojem nevratnosti vývoje makrosystémů je obrovské množství stupňů volnosti (počtů mikrostavů), jimiž se realizují takzvané rovnovážné makrostavy a malé množství stupňů volnosti, jež přísluší nerovnovážným makrostavům, a dále (jak dodávám já) zřejmě subjektivní skutečnost, že mikrostavy generující “rovnovážný” makrostav neumíme rozlišit vzájemně, ale umíme je odlišit od mikrostavů realisujících nerovnovážný makrostav, právě proto, že různé makrostavy stavového prostoru jsou “viditelně” (chcete-li měřitelně) odlišné na rozdíl od různých mikrostavů uvnitř makrostavu – tak, zdá se mi, to Boltzmann myslel!
Nerad bych dále činil to, z čeho viním jiné, a proto dosti všeobecných úvah a pojďme již konečně k podstatě :
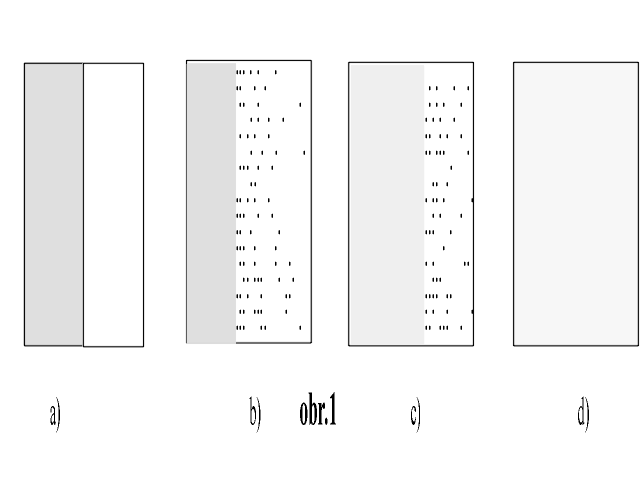
Předpokládejme makroskopický systém vyvíjející se v čase, např. nádobu rozdělenou přepážkou na dvě části, z nichž právě jedna je naplněna plynem, po odstranění přepážky. Na obr. 1a až 1d máme neumělé snímky vývoje systému v určitých okamžicích a máme určit časové pořadí, v němž snímky byly pořízeny. Odpověď založená na experimentální zkušenosti je, že “správné” pořadí je 1a – 1d. Pokusm
e se problém formulovat na mikroskopické úrovni, což nám pomůže uvědomit si jak a zda vůbec lze korektně položit otázku odvoditelnosti tohoto pořadí na základě časově symetrického mikroskopického popisu:Mikroskopický stav isolovaného systému N klasických částic mějme popsán bodem (
r1, v1, . . . , rN, vN) ve fázovém prostoru G . Ovšem snímky na obr.1 neurčují jednoznačně mikrostav X systému, nýbrž pouze velmi hrubý a neostrý obraz X, což je to, co nazýváme makrostavem a označujeme M(X). Každému M(X) přísluší tedy celá oblast mikrostavů GM v G . Pro úplné stanovení G M potřebujeme obvykle s určitou přesností stanovit nějaké makroskopicky konstantní (v isolované soustavě) stavové veličiny, třeba celkovou vnitřní energii, objem apod., ovšem pro kvalitativní analýsu můžeme od této přesné definice abstrahovat. Předpokládejme dále časový vývoj mikrostavů v M(X). Ten je určen klasickými Hamiltonovými rovnicemi, spojujícími jednoznačně X(t0) v daném čase t0 se stavem X(t) v jakémkoliv jiném čase t. Nechť nyní X(t0) a X(t0+Dt) , Dt>0 jsou dva takové mikrostavy. Obrácením (fysikálně nebo matematicky) všech rychlostí v čase t0+Dt dostaneme nový mikrostav. Pokračuje-li nyní vývoj po dobu dalšího Dt, dostaneme se do mikrostavu v čase t0+2Dt, který díky časové symetrii Hamiltoniánu odpovídá stavu X(t0) se všemi rychlostmi opačnými. Tento mikrostav označímeRX = (r1, -v1, . . . , rN, -vN).
Je zřejmé, že patří-li X do
GM, patří i RX do GM, neboť mikrostav RX realizuje makrostav se stejným rozdělením poloh i energiíTi
» ˝ vi˝ 2 , Uij » -rij-1 = -˝ ri - rj˝ -1 , (s omezením na klasický případ)tedy stejný makrostav M(X)
ş M(RX). Nyní jasně vystupují kontury problému se stanovením pořadí snímků na obr. 1 : přechází-li makrostav z M1 v čase t1 do makrostavu M2 v čase t2=t1+Dt , Dt>0 , pak z hlediska fázového prostoru to znamená, že nějaký mikrostav XÎGM1 přechází do nějakého mikrostavu Y v čase t2 takového , že YÎGM2 . Pak ale také RYÎGM2 a pokračujeme-li v časovém vývoji RY opět po dobu Dt, dostaneme stav RX, který ovšem též splňuje RXÎGM1. Takže - čistě ze zákonů dynamiky - existuje-li přechod mezi stavy na obr.1 ve směru a,b,c,d , pak existuje přechod ve směru d,c,b,a ! Je nyní zřejmé, že naše schopnost stanovit “správné” pořadí snímků na obr.1 netkví v zákonech Hamiltonovy dynamiky (které pro tento klasický případ považujeme za zákony přírody). Mé silnější než obvyklé tvrzení lze formulovat takto : Tato “schopnost” je založena na zkušenosti, experimentu a jejich nedostatečnosti a nedokonalosti a tedy nesprávné interpretaci toho, co pozorujeme, tedy je subjektivní a otázka souvislosti této “nevratnosti” s vratností dynamických zákonů je prostě špatně položena, což se pokusím upřesnit.
Nyní jsme připraveni formulovat otázku : jak souvisí nevratnost přechodu mezi makrostavy M
a na obr. 1a a Md na obr. 1d s vratností přechodů mezi dvěma definovanými mikrostavy uvnitř GMa a GMd ? Zdůrazněme, že bez adjektiva definovanými by takto položená otázka ve smyslu formulace problému a) nebyla úplně zadána – neměli bychom jednoznačně stanoveny počáteční podmínky – upozorňuji, že požadujeme získat odpověď ze zákonů dynamiky a statistických úvah.Mějme tvrzení A : “Víme” z experimentu, že přechod Ma®Md se uskuteční a přechod Md®Ma nikoliv.
Mějme dále tvrzení B : Z mechanické analýzy víme, že uskuteční-li se přechod X
a®Xd, kde XaÎGMa , XdÎGMd pak existují RXdÎGMd , RXaÎGMa , tak, že se uskuteční RXd®RXa. Podotázka : Je v tom spor ? “Pododpověď ” : ANO, ovšem proto, že tvrzení A je chybné, nikoliv proto, že by rigorosní analýsa podle B byla chybná !
Totiž :
Co vlastně myslíme experimentálním přechodem M
a®Md ? V jednoduché modelové situaci jako na obr.1 to znamená, že soustava přejde z jednoho z mikrostavů XaÎGMa , v němž se nachází v okamžiku zahájení pozorování, do kteréhokoliv mikrostavu XdÎG Md. Co naopak myslíme experimentálním přechodem Md®Ma ? , Opět tím myslíme, že soustava přejde z jednoho z mikrostavů XdÎGMd , v němž se nachází v okamžiku zahájení pozorování, do kteréhokoliv mikrostavu XaÎGMa. Je-li však velikost oblastí GMa a GMd různá, pak se příslušné experimenty neprovozují za stejných podmínek, a navíc v procesu Md®Ma , jak ukáži dále, příslušný experiment nemodeluje danou hypotézu, což je základní podmínka porovnatelnosti hypotéz. V mezním případě (abstrahujeme-li v prvním přiblížení od rychlostních souřadnic fázového prostoru) postačuje pro experimentální potvrzení hypotézy Ma®Md přechod z jediného existujícího stavu XaÎGMa tak, že považujeme za příznivý případ dosažení jakéhokoliv XdÎGMd , ne nějakého určitého Xd ! Naopak potvrzení hypotézy Md®Ma ověřujeme experimentem s přechodem z jednoho určitého stavu XdÎGMd, v němž se soustava právě nachází ( z mnoha existujících ) , do jediného existujícího stavu XaÎGMa, ale měl by nám stačit přechod z kteréhokoliv možného mikrostavu v Md , aby byly podmínky rovnocenné ! Důvod je prostý , hypotézy Ma®Md, Md®Ma hovoří o stejné fysikální skutečnosti a je proto nutno je ověřovat stejným experimentem . Přesněji, hypotézu Md®Ma neověřuje korektně experiment, kdy sledujeme, zda systém přejde se stavu na obr. 1d do stavu na obr. 1a, protože předpoklad Md v hypotéze Md®Ma znamená, že systém může být ve všech mikrostavech generujících Md (současně !), zatímco v daném experimentu systém startuje vždy z jediného konkrétního mikrostavu uvnitř GMd ! Správně založený experiment by musel přece na vstupní straně zajistit podmínky odpovídající dané hypotéze, tedy současnou existenci všech mikrostavů z GMd (tedy např. bychom místo jedné nádoby s plynem museli použít nejméně N!/((N/2)!)2 nádob, což např. v případě 100 molekul představuje zhruba 1029 nádob – poznámka 2), a pak si troufám tvrdit, že v čase srovnatelném s dobou expanse plynu z jedné poloviny jediné nádoby do celé nádoby tak, aby v obou částech bylo právě 50 molekul , zjistíme v některé nádobě z oněch 1029 samovolnou kompresi všech 100 částic do jedné poloviny). Opačný experiment ovšem opačnou hypotézu ověřuje, neboť hypotéza požaduje přechod z jediného Xa do kteréhokoliv Xd, což v případě příslušného experimentu opravdu postačuje k prohlášení výsledku experimentu za příznivý. A to zanedbávám skutečnost, že obvykle považujeme za dosažení rovnováhy nikoliv stav, kdy je v obou částech nádoby stejný nýbrž pouze zhruba stejný počet molekul, přičemž pravděpodobnosti těchto stavů se liší pro molová množství o mnoho řádů !Kdybychom položili otázku, zda systém přejde z jediného X
a do apriori určeného stavu Xd, pak pravděpodobnost tohoto přechodu bude stejná (stejně malá), jako pravděpodobnost komprese plynu do jedné poloviny nádoby ve směru d®a. Nechtějme ovšem, aby se stejnou pravděpodobností uskutečňovaly různé procesy. Tak, jako dosud nikdo neviděl, aby plyn v nádobě prodělal samovolnou kompresi do jedné poloviny nádoby, stejně tak dosud nikdo neviděl, aby plyn expandoval z jedné poloviny nádoby do celé nádoby tak, aby proces byl zakončen jediným apriori stanoveným mikrostavem (což jsou ekvivalentní experimenty) a právě tak dosud nikdo nerealizoval pokus s N!/((N/2)!)2 nádobami s plynem, aby tak skutečně korektně ověřil hypotézu Md®Ma (mám nejisté tušení, že pro řádově molové množství plynu v nádobě bychom potřebovali alespoň tolik nádob – nebo spíše mnohem více, kolik je atomů v celém vesmíru, takže pro uskutečnění i tohoto jednoduchého experimentu bychom museli mít k disposici přinejmenším 1024 kompletních vesmírů). Doporučuji teď přečíst poznámku 3).S druhou větou to souvisí asi tak, že analogickou analýzu by bylo možno provést v rychlostním prostoru nebo s uvážením příslušného rozdělení energií pro daný typ částic i v kvantové mechanice: stav, kdy dvě dotýkající se pevná tělesa mají různé teploty je realizován mnohem méně mikrostavy, než stav, kdy energie (teplota) je rozdělena rovnoměrně. (To, že vyrovnávání teplot je ekvivalentní toku energie, lze poměrně jednoduše kvalitativně ověřit analýzou pružných srážek, tedy opět užitím Hamiltoniánské dynamiky – zjistíme, že částice s vyšší energií s vyšší pravděpodobností předává energii částici s nižší energií – to určuje tendenci.) Kdybychom opět měli k disposici dostatek vesmírů, bylo by možno realizovat “obří” experiment, kdy by v jednom z 10
X (nějaké obří číslo) současně probíhajících “malých” experimentů došlo během normální relaxační doby k případu nerovnoměrného rozdělení teplot mezi dvěma původně stejně teplými tělesy (při zachování první věty termodynamiky). Tento myšlenkový experiment potvrzuje mou hypotézu o symetrii termodynamických dějů ve stejném smyslu, jako experiment s jedinou dvojicí těles potvrzuje teorii o toku energie ve směru teplotního spádu (čímž, jak tvrdím, nevyvrací vratnost tohoto děje).Tedy závěrem : zdánlivý rozpor mezi vratností základních fysikálních zákonů a
zdánlivou nevratností termodynamických procesů je podle mého názoru pouhým nedorozuměním, protože to, co označujeme za důkaz nevratnosti nějakého termodynamického děje (totiž, že opačný termodynamický děj experiment údajně vyvrací), je dáno pouze tím, že pro onen opačný děj používáme chybně založený experiment, popisující zcela jiný děj. Z toho pak vyplývá mé přesvědčení, že t.zv. “termodynamická šipka času” je pouhou iluzí, kterou naše nedokonalá zkušenost a možnosti pozorování psychologicky spojují s takovými pojmy, jako je jednosměrný tok času a kausalita. (Takže v jistém smyslu mají vlastně autoři [1] pravdu.) Do jaké míry jsou tyto další pojmy objektivně založeny si netroufám posuzovat, právě tak netuším, zda a jak souvisí např. s problémem avansovaných a retardovaných potenciálů v teorii EM pole. Moje tvrzení se týká pouze pojmu termodynamické nevratnosti. Zdá se mi, že v tomto bodě jsou mé úvahy nestandardní v tom smyslu, že jdou dále za závěry učiněné např. v (Lebowitz) [5], a dále též tím, že vrací původní význam Boltzmannovým ideím, který je v pojednáních o statistické fysice obvykle značně zužován ! Sám za sebe se domnívám, že skutečná podstata nesymetrie času bude “ukryta” někde v topologii vesmíru a jeho prostoročasu, a tedy, že klíč záhady drží opět v ruce fysikové (nikoliv však ti “statističtí”, spíše ti “topologičtí”, jako třeba Luboš Motl), a proto ostatní přírodovědci neřkuli filosofové se bohužel pokouší uchopit tento problém za nesprávný konec.Myslím, že pokud jde o kvalitativní odpověď na problém definovaný v odstavcích a) a b), nevidím z mého pohledu šanci, že by se k tomu dalo ještě něco dodat. Je-li tomu opravdu tak, pak je na místě otázka, kde se neustále bere tolik sporů a nepochopení kolem druhé věty termodynamiky a proč tolik fundovaných a nesmírně inteligentních lidí na ní shledává něco magickéh
o.Je vcelku pravděpodobné, že vysvětlení tohoto mého pocitu vyplývá z toho, že problém termodynamické “nevratnosti” se skrývá někde hlouběji, kde ho svým slabým duševním zrakem nejsem schopen zahlédnout ! Tento příspěvek je myšlen nikoliv jako kategorické tvrzení, nýbrž jako výzva k diskusi a mně nezbývá než doufat, že bude takto pochopen a přijat.
V Brně, dne 20.1.1999
Poznámka ( nepodstatná) 1) Vrátím se nyní ke knize [3] a doplním několik obecných postřehů. Autoři [3] (P.Coveney je fysikální chemik, m.j. spolupracoval s I. Prigoginem, nositelem Nobelovy ceny za chemii – za přínos v oblasti nerovnovážné termodynamiky) se domnívají, že podstata jednosměrnosti času – t.zv. “šipka času”- spočívá právě v termodynamice. Tento
předpoklad postulují ihned na počátku knihy, čímž se patrně dostanou do slepé uličky, odkud se jim až do konce nepodaří uniknout. Celé je to dle mého názoru klasickým příkladem podcenění základů fysiky se strany většiny ostatních přírodovědců. Vystavují se tím reálnému nebezpečí, že mnoho jevů v jejich oboru se zajímavými vlastnostmi na úrovni fenomenologické úrovně popisu jim bude připadat “zvláštních, magických či fascinujících” jenom proto, že nerozpoznají jejich elementární fysikální podstatu, ba se mohou domnívat, že jsou s fysikálními zákony v rozporu ! Často pak ztrácí drahocenný čas zkoumáním těchto jevů a snahou popsat je na úrovni jakýchsi t.zv. “emergentních” vlastností nad rámec fundamentálních zákonů. V případě autorů [3] se jim to stalo s periodickými – t.zv. B.Ž. - chemickými reakcemi. Jiným klasickým případem tohoto druhu jsou snahy H.D. Deutsche o teoretickou konstrukci perpetuum mobile, které dosti nekriticky popisuje Otto Exner (rovněž fysikální chemik) v [6]. Nebudu zde tento případ rozebírat, mého tématu se dotýká jen okrajově. Nicméně mohu čtenáři vřele doporučit tento článek, neboť je (naštěstí!) doplněn krásným komentářem Jiřího Langera, který s nenapodobitelnou elegancí a shovívavostí vůči O.Exnerovi uvádí vše na pravou míru.
Poznámka
(technická) 2) Na rozdíl od údaje v [4] myslím, že je to asi 1029 a nikoliv 1030, protože přibližný výraz 2N , který autor asi použil, vyplývá z použití zjednodušené Stirlingovy formule pro faktoriál, která je dobrá pro aproximaci funkce ln(N!) , nikoliv však samotného N! . Její použití ve výrazu pro binomický kombinační faktor N nad k vede k chybě rostoucí s N a pro dané N s min{k,N-k}, takže chyba je největší pro k=N/2, pro niž právě z použití zjednodušené Stirlingovy formule vyplyne přibližný výraz pro kombinační faktor 2N . Zde chyba dosahuje pro N=100 jeden řád a pro N=104 již dva řády. Vtip je v kouzelné vlastnosti funkce ln(x) – pro velká x má tendenci stlačovat několika-řádové chyby na chyby směšně malé : čísla 103008 a 103010 (vyjadřují počet mikrostavů, jimiž se realizuje rovnovážné rozdělení řádově 104 molekul bez uvážení rychlostních souřadnic při přesném a přibližném výpočtu) se liší o dva řády, nicméně jejich logaritmy jsou přibližně 6926 a 6931, takže můžeme bez obav ve vyjádření Boltzmannovy entropie SB=k.lnW použít zjednodušenou Stirlingovu formuli pro logaritmus faktoriálu , ale musíme být moc opatrní , chceme-li pak z takto určené entropie určovat počet mikrostavů jako W=exp(SB/k), neboť se snadno dopustíme chyby třeba několika řádů.
P
oznámka (podstatná) 3) Prohlédněte si prosím schéma zajímavé hry na obrázku dole. Úkolem hráčů A i B je dospět po k tazích do kteréhokoliv koncového bodu na straně druhého hráče, přičemž startují z pevně daného bodu na své straně - hráč B si svůj startovní bod samozřejmě může předem zvolit. Spravedlivé a rovné podmínky, není-liž pravda? Zde kłN-1, kde N je počet sloupců a jednotlivé tahy (to, zda hráč potáhne doprava nebo doleva a nahoru nebo dolů) jsou řízeny náhodným procesem – hodem mince. Pokud byste si stejně jako já vsadili na výhru hráče A spíše než na výhru hráče B, aniž by Vám to připadalo nějak “magické a fascinující”, pak máte můj pohled na problém termodynamické “nevratnosti” jako na dlani.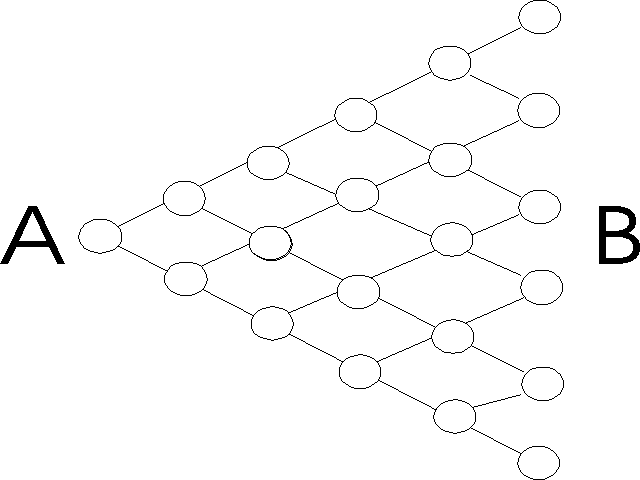
Odkazy :
[1] E.H. Lieb, J. Yngvason, The Physics and the Mathematics of the Second Law of Thermodynamics , archiv LANL http://xxx.lanl.gov/abs/condmat/9708200 , s. 4
[2] E.H. Lieb, J. Yngvason, A Guide to Entropy and the 2-nd Law of Thermodynamics, Notices of the AMS (5/98) archiv AMS http://www.ams.org/notices/199805/lieb.pdf
[3] P.Coveney, R.Highfield, The Arrow of Time (česky v překladu “Šíp času”), Oldag Publishers (1995)
[4] M. Macháček, Encyklopedie fyziky, MF (1995), s. 56
[5] J.L. Lebowitz, Microscopic Reversibility and Macroscopic Behaviour : Physical Explanation and Mathematical Derivations, archiv LANL http://xxx.lanl.gov/abs/condmat/
9605183[6] Otto Exner, Perpetuum mobile stále aktuální ? , VESMÍR ročník 69, s. 55
Poznámka editora: Také jsem četl knihu [3]. Nicméně myslím, že její autoři diskutovali více alternativ podstaty a vzniku nevratnosti dějů, než jen "termodynamickou", tedy jakousi fenomenologickou. Statistickým přístupem se také zabývali, i když ho zproblematizovali tzv. problémem "hrubozrnného dělení". Psalo se tam i o nevratnosti procesu měření v kvantové mechanice, který participuje v jejích v zásadě vratných rovnicích. Také na mikročásticové úrovni se tam diskutoval časově asymetrický děj - anomální rozpad Kaonu nula. Tato kniha je v současnosti k dostání ve výprodejích ve středu města, doporučuji se s ní seznámit.