1. Co je fraktál, fraktálová dimenze (rozměr), fraktální jazyk přírody

+Obyčejné, hladké geometrické útvary - celočíselná dimenze

"Normální" útvary kolem nás se dají popsat nebo zobrazit pomocí jistého konečného počtu obrázků či parametrů, které je charakterizují. Každý z nás intuitivně ví, jak vypadá krychle, koule, čtverec, přímka, rovina. Víme také, jak vypočítat délku, plochu či objem těchto útvarů (většinou se jedná o jednoduchá násobení či součty) - výsledkem je vždy konečné, konkrétní číslo, ať se to počítá jakkoliv, z libovolně malých dílků.

Podobně můžeme spočítat tyto veličiny i u libovolné "rozumné" kombinace těchto elementárních útvarů, stejně jako u křivky, plochy apod. libovolně zakřivené, ale v jistém smyslu "normální", tj. např. hladké. (elipsy, hyperboly, paraboly). Těmto útvarům můžeme přiřadit jisté celé číslo, které se nazývá POČTEM ROZMĚRŮ či DIMENZÍ DANÉHO ÚTVARU. Takže "hladká" přímka či křivka má dimenzi 1 (je jednorozměrná- poloha bodu na nich je charakterizována JEDNÍM číslem - souřadnicí), hladká "sebezprohýbanější" plocha má dimenzi 2, krychle, koule, válec či běžný prostor kolem nás mají dimenzi 3, protože poloha každého bodu v nich je jednoznačně určena třemi čísly - souřadnicemi.

Všimněme si, že např. poloha nějakého místa na "kulaté" Zemi je určena také 3 čísly - zeměpisnou šířkou, zeměpisnou délkou a ještě nadmořskou výškou, tedy vystačíme se třemi souřadnicemi, protože náš prostor, který známe z vlastní zkušenosti, má 3 rozměry. A všechny běžné utvary v něm maji dimenzi buď 1,2,3 nebo - 0 (to platí pro bod, protože polohu jakéhokoliv prvku "v něm" není třeba určovat žádným číslem).

+Nekonečně členité útvary - FRAKTÁLY - fraktální (neceločíselná) dimenze

Je proto velmi zajímavé, že existují ještě jiné (geometrické) útvary, které však nejsou pouhým plodem abstraktní fantazie matematiků, ale mají své vzory přímo v přírodě.

Vezměme si například, jak vypočítat délku pobřeží nějakého reálného ostrova. Máme-li linii pobřeží znázorněnu na nějaké mapě např. měřítka 1:100 000, pomocí třeba kružítka můžeme přibližně "kopírovat" tuto linii a přenést ji na lineární (přímé) pravítko. Budeme-li mít nějakou podrobnější mapu, např. měřítka 1: 1000 a provedeme-li stejný proces s kružítkem, výsledkem bude větší hodnota TÉ SAMÉ DÉLKY pobřeží. Dokonce délka jakéhokoliv úseku tohoto pobřeží bude zpravidla větší. Důvod je zřejmý - ve větším měřítku jsme neviděli všechny skutečné zákruty, členitosti a nepravidelnosti onoho pobřeží. Když toto pobřeží obejdeme v reálu pěšky, získáme ještě větší délku toho samého útvaru a pokud bychom se stali mravenci a museli kopírovat ještě menši členitosti a nemohli bychom si např. cestu přes balvan krátit cestou po přímce, naše "nejkratší možná cesta v daném měřítku", tedy příslušná vzdálenost by byla ještě větší a co víc, se zmenšujícím se měřítkem by mohla růst vlastně do nekonečna, pokud bychom se někdy v zmenšování měřítka nezastavili! Čili ostrov o konečné ploše má nekonečnou délku pobřeží - jak šokující !

Když si vzpomeneme, že délka jakékoliv "rozumné" křivky, která má dimenzi jedna (můžeme ji napodobit třeba nití) , se blíží při podobném procesu měření v různých měřítkách nějakému KONEČNÉMU číslu, hned vidíme rozdíl. Naše nekonečně "kostrbaté" pobřeží musí rozhodně zabírat v rovině více místa, musí v ní být poněkud hustší, než "obyčejná" hladká a jednorozměrná křivka, avšak zabírá zároveň méně místa, než dvojrozměrný, tedy plošný útvar. Pokud tedy nějaký útvar svojí důležitou vlastností leží "mezi" útvarem jednorozměrným a dvojrozměrným, očekávali bychom, že bude existovat nějaký parametr mezi 1 a 2, který bude mít asi charakter dimenze a bude roven 1 a 2 pro ony zmíněné "normální útvary". Ukazuje se, že je tomu skutečně tak a že tento parametr souvisí s různou rychlostí, s jakou "délka" oněch "podivných" křivek roste nad všechny meze do nekonečna. Tato zobecněná, neceločíselná dimenze, se nazývá fraktální dimenzí (nebo též podle objevitele tzv. "Hausdorffovou dimenzí") - od slovního základu "frakce" čili zlomek, úlomek, něco "necelého" a útvary, které mají tuto neceločíselnou dimenzi, se nazývají FRAKTÁLY.

Nutno říci, že tyto představy se neomezují na rozměry od 1 do 2, např. při zkoumání různých nekonečně členitých hor či mraků se usoudilo, že jejich fraktální dimenze se nacházejí mezi 2 a 3, protože si je můžeme přiblížit pomocí systému maličkých plošek, které se však při bližším pohledu rozdělí do ještě menších systémů plošek atd. atd. Takže členitost při zvětšování měřítka zůstává stále PODOBNÁ struktuře z menších zvětšení. Tato takzvaná SOBĚPODOBNOST (nikoliv stejnost!) fraktálních útvarů je vlastně hlavním jejich znakem a většinou je také považována za jejich definici. Tuto přítomnost podobných ůtvarů při zvětšování detailů nenajdeme na klasických, elementárních útvarech, jako jsou na začátku zmiňované krychle, koule, čtverce apod.

Když zvětšíme nějakou kouli, neuvidíme v ni menší kulové struktury apod.

Je ovšem pravda, že pomocí těchto elementárních tvarů, jako jsou úsečky, trojúhelníky, čtverce, koule, kříže apod. , a jejich nekonečným zmenšováním a vnořováním můžeme fraktální útvary "uměle vyrobit" a napodobit tak přírodu, která je už vlastně dávno zná. Princip opakování podobných tvarů v zmenšené podobě je vidět nejen u neživých útvarů, ale i u živých organizmů a jejich skupin, prakticky u jakékoliv komplexní, složité struktury, která je vytvářena i pomocí VELMI JEDNODUCHÝCH PRAVIDEL. Způsob, jakým probíhá větvení stromů (silnější větve se rozbíhají ve stále menší a tenčí větvičky) či cév a žil v tělech živočichů nebo hromadění např. baktérií a řas v koloniích a možná i tučňáků na ostrovech v polárních mořích se dá popsat jediným nástrojem: jazykem fraktální geometrie.

Tento jazyk je však schopen vysvětlit ještě více: slouží nejen k pochopení morfologie složitých statických prostorových struktur, ale je schopen pojmout i složité děje, které se odehrávají v čase, tedy jevy DYNAMICKÉ. Uvidíme, že princip koexistence jednoduchých výchozích pravidel a komplexního, složitého výsledného tvaru platí i zde. Lze jej chápat i jako princip koexistence řádu a chaosu v jediném objektu.

2. Fraktální geometrie potkává teorii chaosu ("podivné" atraktory dynamických systémů)

Fyzikální soustavy při svém vývoji v čase opisují různé dráhy-grafy v prostoru - proto je možno je dobře "zviditelňovat" na počítačích. Pro pohyb jednoho idealizovaného hmotného bodu vystačíme s 3 - rozměrným prostorem jeho souřadnic (když zahrneme ještě 3 složky jeho vektoru rychlosti, bude jich 6- to je tzv. fázový prostor), při pohybu pevných, pružných a kapalných těles, které obsahují bodů daleko víc, musíme sáhnout k matematické abstrakci vícerozměrných (někdyi nekonečněrozměrných) prostorů, které si neumíme přímo vizuálně představit, ale matematicky a počítačově se dají v principu zvládnout, někdy se dokonce daří počet dimenzí fyzikálních problémů znatelně snížit.

Klasická mechanika popisovala systémy, jejichž dráhy se daly vyjádřit pomocí přesných deterministických vzorců a byly v podstatě ekvivalentní hladkým a "normálním" tvarům klasické geometrie s celočíselnou dimenzí. Rovnice, které popisovaly chování těchto systémů či těles, byly většinou (i když ne vždy) lineární, tj. jednotlivé veličiny v nich byly navzájem přímo úměrné. Vzájemné silové působení v těchto soustavách bylo také tak "rozumné", že nevedlo k příliš velkým a nespojitým, náhlým a nepředpověditelným nestabilitám. Triumfem klasického determinismu byly úspěchy mechaniky nebeských těles, pohybů planet kolem Slunce či jednodušších hvězdných systémů - čili pohyby pod vlivem gravitačního pole.

Avšak už od konce minulého století klasická mechanika (a dynamika vůbec) začala narážet na vážné potíže. Zatímco pohyb soustavy dvou hmotných těles (např. Slunce a Jupitera) bylo možno vypočítat pomocí vzorců (tzv. analyticky) a tyto výsledky souhlasily skvěle s realitou, už výpočet pouhých 3 těles s porovnatelnou hmotností vedl ke krizi mechaniky - bylo dokázáno, že analytické řešení neexistuje!!! Čili není možno teoreticky spočítat a tedy předpovědět dráhy například soustavy 3 blízkých hvězd o stejné hmotnosti. V řešení tohoto problému byly objeveny podivné nestability, které vedly k chaotickému chování u záležitosti, která sama o sobě nijak chaotická či náhodná nebyla (rovnice byly striktně dány). Chaotické chování se začalo rozpoznávat i jinde - u turbulentních (vířivých) pohybů kapalin, u vývoje populací různých živočichů, ekologických systémů vůbec, u vývoje počasí a klimatu, a na mnoha dalších místech. Každý z nás zná situaci, když meteorologům nevyjde jejich předpověď, počítaná na skvělých počítačích a člověk přesto zmokne, i když mělo být třeba úplně jasno. Jakmile se však v příslušných meteorologických a jiných rovnicích vyskytne velká míra vzájemného ovlivňování uvnitř systému (což je vyjádřeno značnou mírou nelinearity těchto rovnic), nelze se spolehnout na sebelepší počítače. Proč? Protože sebemenší změna teploty, tlaku či hustoty vzduchu a rychlosti větru vede ke značně odlišnému vývoji v budoucnosti.

Proto nelze v principu předpovídat budoucnost většiny složitých jevů a systémů a zejména ne lidských osudů či světa jako takového. Z tohoto hlediska se jeví praxe věštců, kartářek, jasnovidců a astrologů jako naprosto pochybná, vždyt pouhá banánová slupka může s vaším osudem zamávat více než vzdálené hvězdy nebo jakési "předurčení". Teorie chaosu ve skutečnosti vypovídá o tom, že cosi jako předurčení nemůže v složitých jevech vůbec existovat.

Tento zneklidňující fakt má však i pozitivní líc - jelikož nejsme předurčeni, máme značnou svobodu pohybu, myšlení, jednání a je hlavně na nás, jaký bude náš "osud".

Citlivost vývoje a dynamiky na nepatrné změny (či výchylky) na počátku bývá označována jako "Motýli efekt". V některých případech je totiž možné i to, že když motýl mávne slabě křídly třeba v Austrálii, může to vyvolat o týden později (v původně nehybné atmosféře) tornádo o mnoho tisíců kilometrů odtud. V praxi je však tento efekt přehlušen daleko silnějšími vlivy, než je motýlí mávnutí, samozřejmě, v neposlední řadě vlastní dynamikou atmosféry. Je však pohyb atmosféry skutečně naprosto chaotický? Opravdu neexistuje nic, co by aspoň trochu rozhodovalo o budoucnosti počasí, o budoucnosti vývoje populací, co by k sobě přitahovalo jejich vývoj? Odpověď zní: ano, takové útvary existují, nejsou však tak jednoduché, jak jsme byli zvyklí z klasické fyziky a matematiky či geometrie.

+Co přitahuje dynamické systémy na jejich dráze, Lorenzův "podivný" atraktor

Při hraní kuliček se soutěží o to, kdo jich "pošle" víc do důlku. Kalkulujeme jako se samozřejmostí, že kulička, poslaná jemně do důlku skončí na jeho dně, že je tam jakoby "přitahována". A skutečně, ve fyzice se nejnižší bod prohlubně, kde kulička skončí, nazývá atraktorem. Atraktorem je však jakákoliv množina, kam jeví i jakékoliv jiné těleso tendenci směřovat či se v něm trvale pohybovat. V případě planety, pohybující se kolem Slunce je tímto atraktorem buď kružnice, nebo elipsa čili sympaticky názorné, hladké křivky o konečné délce, které se dokonce brzy uzavírají, takže v nich je planeta najisto trvale vázána. Podobné křivky či ůtvary jsou atraktorem jakéhokoliv jednoduchého systému klasické nechaotické fyziky, chemie či biologie. Například pokud je dráha rovinného kyvadla s malými výchylkami pozorována ve 2-dimenzionálním fázovem prostoru jeho úhlové výchylky a rychlosti této výchylky, vidíme jako permanentní jeho dráhu opět kružnici. U stabilních systémů dokonce tyto atraktory "přitahuji" všechny stavy ve svém blízkém okolí.

V polovině 60. let byl meteorolog Edward Lorenz postaven před tento úkol: spočítat numericky na počítači tehdejší úrovně vývoj jistého velmi zjednodušeného modelu počasí (vyjádřeného poměrně stručnými rovnicemi a jistými parametry charakteru konstant) , které mělo pouze 3 proměnné, měnící se v čase. Byl velmi překvapen nestabilitou a chaotickým vývojem tohoto meteorologického modelu, protože s velmi nepatrnými změnami výchozích dat se dostavovaly zcela rozdílné meteorologické výsledky. Ani zmenšování diferencí dat na jakoukoliv úroveň leckdy nevedlo ke zvýšení spolehlivosti předpovědi. Odhalil však, že přesto se vypočtená "dráha" vývoje pohybuje v rámci jistého podivného útvaru (viz obrázek?). Vzhledem k tomu, že tento atraktor, který na sebe vázal řešení tohoto chaotického povětrnostního modelu neměl charakter "normální" křivky, která by se uzavírala a nebo by se alespoň dala popsat vzorcem, byl označen slovem "podivný". Později se zjistilo, že tento podivný atraktor je FRAKTÁLEM a je to "křivka" o nekonečné délce, obsažená v konečném prostorovém objemu! Při některých parametrech Lorenzových rovnic je fraktální dimenze jeho atraktoru o něco větší než 2!

Nutno říci, že chaotické atraktory jsou z velké části fraktály, že však ne všechny fraktály jsou chaotické - příkladem je např. Sierpinskeho trojúhelníková krajka, křivka von Kochové, Cantorův prach (diskontinuum) aj.. Kritériem fraktálnosti je SOBĚPODOBNOST, nezávislost tvaru na velikosti měřítka, což nevylučuje pravidelnost (ale ani ji to nevyžaduje ). Avšak soběpodobnost chaotických fraktálů je jistým druhem řádu, který je znakem deterministického chaosu.

Fraktálová struktura se objevuje i u tzv. diagramů BIFURKACÍ, což je větvení vlastností rovnic při změně parametrů, je to extrémní případ nestability, kdy jedna a ta samá situace má 2 různá, rozbíhající se řešení.

Nejznámější fraktál -
3. Mandelbrotova množina - dynamika umocňování komplexních čísel
aneb Z na druhou plus C, to celé pořád dokola; "ZOOM" dovnitř

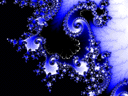Obraťme však svou pozornost k ještě jednoduššeji utvořenému fraktálu, který vzniká při "nevinném" opakovaném umocňování čísel, a to čísel komplexních (komplexní čísla jsou jistým zobecněním reálných čísel, která známe např. z pravítek -fakticky jde o rozšíření této oblasti o druhou - tzv.imaginární dimenzi, prostřednictvím imaginární jednotky I , což je symbolická odmocnina z čísla "-1", která není "reálným číslem", avšak přesto má důležité aplikace v matematice, fyzice a inženýrství).

Jednoduché umocnění čísla na druhou a přičtení jistého konstantního komplexního čísla C je základní krok tohoto algoritmu. Za první Z se bere u Mandelbrotovy množiny nula, další je výsledek prvního kroku, tj. 0 na druhou + C = C, když toto podrobíme onomu konstantnímu výpočetnímu kroku, dostaneme C na druhou + C atd. Výsledkem je, že C hodně vzdálené od nuly rychle "míří" k nekonečnu, ty blízké k nule naopak míří k nule. Tyto tendence se vyrovnávají v jistém hraničním pásu, který však při bližším prozkoumání má nekonečně jemnou strukturu. (tento hraniční pás obsahuje zhruba řečeno body, které ani "neulétávají" do nekonečna, ani "nekolabují" k nule, ale víceméně se většinou pohybují stále uvnitř hraničního pásu - je to vlastně chaotický atraktor onoho zacykleného početního procesu).Abychom tuto strukturu zviditelnili, přiřadíme rozdílnému chování bodů různé barvy z celé barevné palety. To všechno pak můžeme shlédnout na grafickém výstupu nějakého standartního fraktálového programu (např. FRACTINT), který má zpravidla kreslení "mapy" Mandelbrotovy množiny v sobě zabudováno. To, že tato členitá struktura nemizí při jakémkoliv zvětšení, si můžeme ověřit ZOOMOVÁNÍM, čili zvětšováním jakýchkoliv míst v tomto fraktálu.

Občas zahlédneme i víceméně podobnou repliku celé Mandelbrotovy množiny, takže vidíme, že bychom se do ní mohli skutečně nořit do nekonečna.

Drobnou modifikací uvedeného postupu bychom ještě získali systém fraktálních Juliových množin, z nichž každá se vztahuje k jednomu každému konkrétnímu bodu Mandelbrotovy množiny, ale to bychom už zabíhali do podrobností...

Struktura Mandelbrotovy množiny je velmi složitá a její matematické zkoumání je velmi náročné (existují však ještě daleko složitější chaotické či fraktální objekty). I pouhý pohled na ni nám však leccos dá.

Pokračování v dalších číslech...

Pavel -Lithium- Vachtl